Bayesian Decision Theory

· by · in Machine Learning, Statistics. ·
Bayesian Decision Theory (BDT), also known as Bayesian Hypothesis Testing and Bayesian inference, is a fundamental statistical approach that quantifies the tradeoffs between various decisions using distributions and costs that accompany such decisions. In pattern recognition it is used for designing classifiers making the assumption that the problem is posed in probabilistic terms, and that all of the relevant probability values are known. Generally, we don’t have such perfect information but it is a good place to start when studying machine learning, statistical inference, and detection theory in signal processing. BDT also has many applications in science, engineering, and medicine. A decision can be viewed as a hypothesis deciding where observations of the random variable Y come from. For instance, in image analysis you may want to decide if a picture is of a cat or a dog, in medicine you want to see if heart beat is nominal or irregular, or in radar may want to decide if a target is on the map or not. 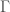We assume two possible hypotheses H_{0} (null hypothesis) and H_{1} (alternate hypothesis) corresponding to two possible probability distributions P_{0} and P_{1} on the observation space \Gamma. We write this problem as H_{0}: P_{0}(y) versus H_{1}: P_{1}(y). 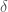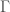A decision rule \delta for H_{0} versus H_{1} is any partition of the observation set \Gamma into sets \Gamma_{0} and \Gamma_{1}=1- \Gamma_{0}. We think of the decision rule as such:
\delta(y) = \left\{ \begin{array}{ll} 1 if y \in \Gamma_{1}\\ 0 if y \in \Gamma_{0} \end{array} \right.
We would like to optimize how we choose \Gamma_{1} so to do so we assign costs to our decisions, which are some positive numbers. C_{ij} is the cost incurred by choosing hypothesis H_{i} when hypothesis H_{j} is true. The decision rule is alternatively written as the likelihood ratio L(y) for the observed value of Y and then makes its decision by comparing this ration to the threshold \tau:
 \delta(y) = \left\{ \begin{array}{ll} 1 if L(y) \geq \tau \\ 0 if L(y) < \tau \end{array} \right.
where
L(y) = \frac{p_{1}(y)}{p_{0}(y)} and \tau = \frac{\pi_{0}(C_{10}-C_{00})}{\pi_{1}(C_{01}-C_{11})}
We then define the conditional risk for each hypothesis as the expected (average) cost incurred by the decision rule 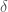\delta when that hypothesis is :
R_{0} = C_{00}P_{0}(\Gamma_{0})+C_{10}P_{0}(\Gamma_{1})
R_{1} = C_{11}P_{1}(\Gamma_{1})+C_{01}P_{1}(\Gamma_{0})
R_{0} is the risk of choosing H_{0} when  H_{1} is true multiplied the probability of this decision plus choosing H_{1} when  H_{0} is true multiplied the probability of doing this. Next we assign priori probability \pi_{0} that  H_{0} is true unconditioned of the observation, and we assign priori probability \pi_{1} = 1- \pi_{0}  that  H_{1} is true. Given the risks and prior probabilities we can then define the Bayes Risk which is the overall average cost of the decision rule:
r(\delta)= \pi_{0}R_{0}(\delta)+ \pi_{1}R_{1}(\delta)
The optimum decision rule for H_{0} versus H_{1} is one that minimizes over all decision rules the Bayes risk. Such as rule is called the Bayes rule. Below is a simple illustrative example of the decision boundary where p_{0} and p_{1} are Gaussian, and we have uniform costs, and equal priors.
Capture

Leave a comment